Quantum Error Correction
Introduction
Quantum Computers have a lot of potential as the next generation of computing devices. Earlier this year Google demonstrated that their Quantum computers have achieved supremacy over existing classical computers on some very specific tasks. We are now in the NISQ (Noisy-Intermediate-Scale-Quantum-Computing) Era where the Qubits (The analog of bits) are imperfect and operations are noisy. One of the technological hurdles to overcome before we have full-fledged Quantum Computers is to detect and mitigate these noises from our computation and reverse them. That is the challenge of Error Correction. Surprisingly ideas from this field have cropped up in areas of physics like Condensed Matter Physics and Quantum Gravity! In this post, I will try to introduce some key concepts in Quantum Error-Correcting Codes..
Why the Noise?
There are mainly three sources of errors in quantum computation.
These errors can be further classified as coherent or incoherent errors. Gate Errors and measurement errors can be reduced by improvements in Hardware.
Coherent Errors

Figure 1. Illustration of a coherent error on the Bloch sphere.
Coherent errors do not destroy the coherence of a state. They introduce slight unitary perturbations to the ideal quantum states. These Errors accumulate through the course of the computation and can limit the depth of a Quantum Circuit. Pure states always live on the surface of the Bloch sphere and every coherent error maps pure states to pure states.
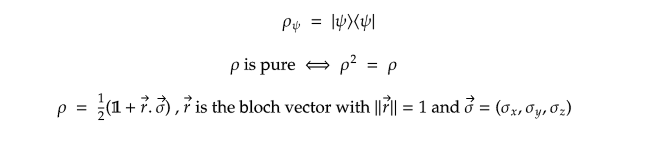
Incoherent Errors
Incoherent errors destroy the coherence of a quantum state, i.e it maps pure states to mixed states. Mixed states are probabilistic mixtures of pure states. Mixed states can be represented by points living inside of the Bloch sphere.

Incoherent errors occur due to the interaction of the qubits with the environment. This interaction results in leaking of information to the environment by a process called decoherence. It destroys the quantumness of our qubits. The more number of qubits there are, the more probable that decoherence occurs. This is the reason why we don’t observe weird superpositions in our daily life. Such incoherent errors can be mathematically modeled by the so-called Kraus -Sudarshan Maps.
Why decoherence?
When a quantum system (e.g., the qubits on a quantum processor) is not perfectly isolated from its environment it generally co-evolves with the degrees of freedom in the environment(e,g., the surrounding gas molecules in the environment or stray magnetic fields). The implication is that even though the total time evolution of the system and environment is unitary, restriction to the system state generally is not. Superposition for subatomic particles is like balancing a coin, any small movement, vibration or even sound can affect the coin from being in a neutral state to collapsing on either heads or tails (0 or 1). Due to decoherence qubits are extremely fragile and their ability to stay in superposition and or entangle is severely jeopardized. Radiation, light, sound, vibrations, heat, magnetic fields or even the act of measuring a qubit are all examples of decoherence. Coherence Length is the time a qubit can survive its quantum properties. The world’s longest-lasting qubit holds the record of 39 minutes in a superposition state, it may seem short but that amount of time could calculate more than 200 million operations. Now the idea is to have a qubit system with a coherence length long enough to compute mathematical problems. Eventual decoherence is an inevitable phenomenon, even then we can prolong the coherence length by Quantum Error Correction.
Measurement Error Mitigation
The effect of noise that occurs throughout a computation will be quite complex in general but a simpler form of noise is that occurring during final measurement. At this point, the only job remaining in the circuit is to extract a bit string as an output. For an n qubit final measurement, this means extracting one of the possible 2ⁿ bit strings. As a simple model of the noise in this process, we can imagine that the measurement first selects one of these outputs in a perfect and noiseless manner, and then noise subsequently causes this perfect output to be randomly perturbed before it is returned.
Given this model, it is very easy to determine exactly what the effects of measurement errors are. We can simply prepare each of the 2ⁿ possible basis states, immediately measure them, and see what probability exists for each outcome and invert them.
Quantum Error-Correcting Codes (QEC)
“We have learned that it is possible to fight entanglement with entanglement.”
– John Preskill
Figure 2. The landscape of Fault Tolerance by Daniel Gottesman
Even though these errors can be reduced by better and better Hardware capabilities, one cannot hope to completely eradicate them because to do so we would have to completely isolate our Quantum Computer from the outside world to shield from decoherence. Doing so would mean that we would not be able to read out the results of our computation, which will give us a perfectly good but useless computer. This is why we need to develop other clever ways of keeping the errors in check. There already exists a theory of error correcting codes for classical computers developed by Shannon,Hamming and others. The theory of Quantum Error Correcting codes borrows ideas from them for the Quantum Domain.
3 Qubit Repetition Code
This is the most trivial Quantum Error Correcting Code, but can illustrate the basic idea of error correction. Suppose Alice and Bob want to communicate a qubit of information. Unfortunately the transmission lines are faulty and will flip the qubits( i.e act by a X – operator ) with probability ‘p’. This situation is analogous to the case of decoherence.
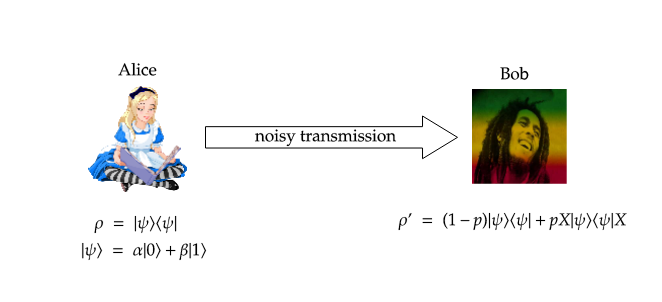
The data Bob receives will be corrupted with probability ‘p’. If Alice does a repetition of her data before transmission one of 8 scenarios can play out. The encoding is a spreading out of information about Alice’s qubit onto a highly entangled set of 3 Qubits. This is a typical feature of all error-correcting codes. The subspace spanned by this set of entangled basis states is called the codespace(C) of the Code. The encoding procedure can be visualized as follows.
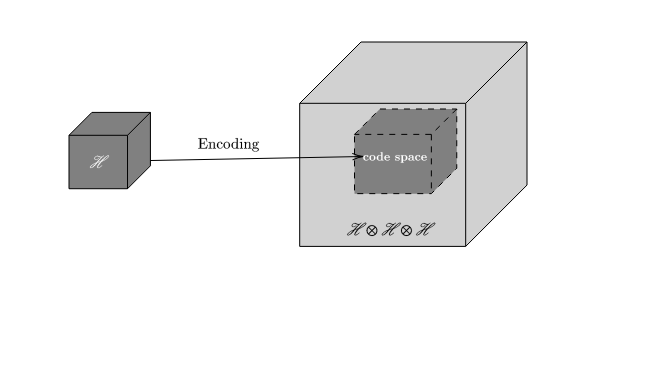
Figure 3. Visualization of the encoding procedure.
The set of possible errors that can happen along with their probabilities,

after receiving the qubits, Bob can detect the position of the error by measuring the Z⊗Z⊗I and I⊗Z⊗Z which are called the syndromes.

If only a maximum of single bit flip occurs Bob can identify the position of the bit flip by measuring the eigenvalues of the syndromes. The group generated by the syndromes under composition is called the stabilizer of the code. All valid codewords will have eigenvalue 1 for all elements of this group. Bob can measure the syndromes using two ancilla qubits. First perform two CNOT’s from the first and second qubit to the first syndrome qubit, followed by two CNOT’s from the second and third qubit to the second syndrome qubit.
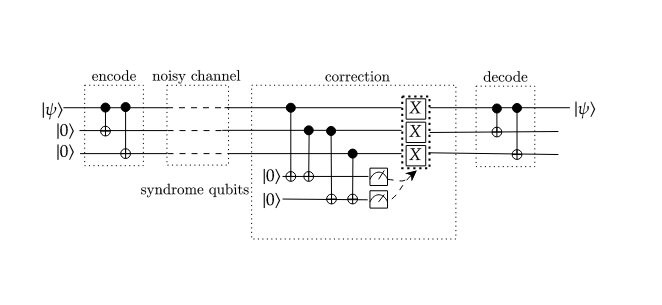
Figure 4. Circuit diagram for the 3 – qubit repetition code

this scheme can correct errors with a maximum of 1-bit flip. The success probability of this scheme
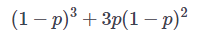
is and fails with a probability,
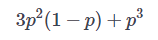
For low ’p’ this can work pretty well. Thus using this procedure Alice and Bob can reduce the chance of their data getting corrupted while transmission. But this is not a General Error Correcting code since it can only protect the data against bit-flip errors. In the quantum domain, there are other types of Errors like Z – error ( phase flip) and Y errors. A general Error-correcting code should be able to correct all of these errors simultaneously.


Ashwanth Krishnan